Töne, Frequenzen, Harmonie, Instrumenten-Stimmungen
In Raum und Zeit gibt es Vorgänge, die sich zyklisch wiederholen. Diese bezeichnen wir als Schwingungen.
Schwingungen entstehen immer dann, wenn Energie zwischen zwei verschiedenen
energetischen Zuständen (Polen) hin und her pendeln kann.
Eine Schwingung ist ein sich periodisch wiederholender Vorgang.
Beispiele:
- drehendes Rad
- schwingendes Pendel
- vibrierendes Sprungbrett
- hoch und runter an einem Punkt einer Wasserwelle
- hoch- und runterschwingendes Gewicht an einer Feder
- hörbarer Ton mit einer bestimmten Tonhöhe
- Licht mit einer bestimmten Farbe
usw.
Unser ganzes Dasein in der materiellen Schöpfung ist mit Schwingungen verbunden.
Oft sind wir Menschen wie verstimmte Instrumente, die nicht mehr harmonisch schwingen.
Es gibt viele Möglichkeiten, wie wir unsere Instrumente wieder stimmen.
Eine davon ist die Arbeit mit harmonischen Frequenzen.
Diese harmonischen Frequenzen finden wir vor allem in der unberührten Natur.
Beispiele:
- harmonische Farben und Strukturen (heilige Geometrie) bei Pflanzen oder Tieren
- harmonischer Aufbau von Lebewesen und deren Wandel im Lauf der Zeit (Wachstum und Entwicklung)
- harmonische Klänge (Vogelzwitschern) oder Geräusche (Sturm, Meeresbrandung, Rauschen eines Wasserfalles)
Diese Schöpfung können wir mit technischen Mitteln nur nachahmen.
Es ist jedoch von Vorteil, wenn wir die Natur genau beobachten
und die Prinzipien des Lebens für uns anwenden.
Wenn wir in der göttlichen Harmonie sind,
geschieht dies von ganz alleine.
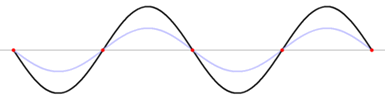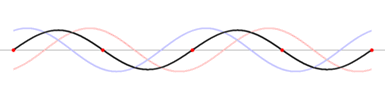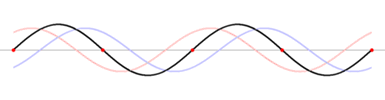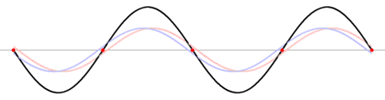
Bei Schwingungen auf Saiten oder anderen begrenzten Medien (z. B. Fensterscheibe, Wasserkrug, Stab, Kugel,
Quader, Stimmgabel) bilden sich beim Anschwingen immer stehende Wellen. Das folgende Bild macht
anschaulich deutlich, wie durch die Überlagerung einer nach rechts laufenden Welle (blau) und einer nach
links laufenden Welle (rot) in der Summe eine stehende Welle (schwarz) gebildet wird. Bei der stehenden Welle
gibt es fest stehende Knoten und bewegende Schwingungsbäuche. Es scheint so, als würde sich die stehende Welle (schwarz) nicht
nach links oder rechts bewegen. Dies kommt jedoch durch die Aufhebung der nach links (rot) und rechts (blau) laufenden Wellen.
Bildquelle
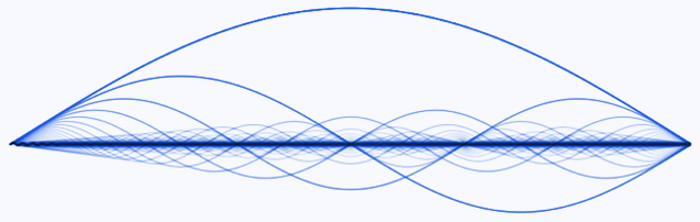
Bei der Bildung von stehenden Wellen in begrenzten Medien entstehen auch immer Oberwellen
mit höheren Harmonischen, bei denen immer mehr Knoten auf der Nullinie auftauchen.
Grundschwingung und Oberschwingungen einer Saite (siehe auch hier)
Die Frequenz einer Schwingung = Anzahl der Schwingungsperioden pro Zeiteinheit (Sekunde)
Die Physik der Schwingungen: animierte Saitenschwingung --> Loaded String Applet starten
In diesem Video wird nacheinander immer der gleiche Ton (C mit 128Hz) auf verschiedenen Instrumenten
gespielt und die Frequenzen in Echtzeit in einem Spektrogramm dargestellt. Der Grundton und die Obertöne sind immer
bei den gleichen Frequenzen (Grundfrequenz: 1x 128Hz, Obertöne: 2x, 3x, 4x, 5x, 6x, 7x, usw.). Der unterschiedliche
Klang bei Instrumenten oder auch menschlichen Stimmen entsteht durch die verschiedenen Intensitäten bei den
Obertönen und aus deren zeitlichen auf- und abschwellen, die oft so komplex wie ein Fingerabdruck sind.
weitere Bilder von Spektrogrammen: Grundton und Obertöne
Was steckt hinter dem Begriff Oktave?
Das Unendlichkeits-Symbol Ꝏ sieht wie eine liegende 8 aus.
Es ähnelt auch einer Saite, die mit 2 Schwingungsbäuchen und einem Schwingungsknoten in der Mitte schwingt.
So eine Schwingung hat genau die doppelte Frequenz der Grundfrequenz und liegt eine Oktave höher (Verhältnis 2 / 1).
Wellenlänge und Frequenz verhalten sich immer umgekehrt proportional. Eine kleinere Wellenlänge führt zu einer größeren Frequenz und umgekehrt.
Wellenlänge * Frequenz = konstant = Schallgeschwindigkeit im Ausbreitungsmedium
Die Grundfrequenz ist die niedrigste Frequenz auf einer schwingenden Saite, hat die größtmögliche Wellenlänge und keine Schwingungsknoten.
Die Schwingung eine Oktave höher hat die doppelte Frequenz, die halbe Wellenlänge und einen Schwingungsknoten genau in der Mitte der Saite.
8 - Acht - okta - Oktave - Unendlichkeits-Symbol Ꝏ - verbindet Alpha α (Anfang) und Omega Ω (Ende)
Eine Oktave höher bedeutet immer eine doppelt so hohe Frequenz.
Eine Oktave niedriger bedeutet immer eine halb so hohe Frequenz.
Diese Verdopplung und Halbierung kann unendlich fortgesetzt werden.
Eine gespannte Saite mit einer bestimmten Masse (Dicke), Zugfestigkeit
und Spannkraft schwingt immer mit einer bestimmten Frequenz.
Dies wird bei Saiteninstrumenten verwendet (z. B. Gitarre).
Angenommen, eine Saite wird auf ein A mit 440 Hz gestimmt,
dann schwingt die Saite beim anzupfen mit dieser Grundfrequenz.
Wird die Seite genau in der Mitte gedrückt (12. Bund der Gitarre), so dass nur noch eine Hälfte
der Seite schwingen kann, dann verdoppelt sich die Tonhöhe um eine Oktave auf 880 Hz.
Eine Halbierung der Saitenlänge bedeutet eine Verdopplung der Frequenz.
Diese Halbierung könnte theoretisch bis ins Unendliche fortgesetzt werden, wobei sich
die Frequenz jeweils verdoppeln würde, nur ist der Hörbereich des Menschen begrenzt.
Der Mensch kann je nach Alter und Gehör Töne im Bereich von 20 Hz bis 20000 Hz hören.
Neben der Grundfrequenz werden auch immer höhere Harmonische angeregt,
die den Klang und die Einzigartigkeit von Instrumenten und auch der Stimme ausmachen.
Bei einer Saite entstehen die höheren Harmonischen, wenn die Saite bei der Schwingung
1, 2, 3, 4, 5, 6, 7, ... Schwingungsknoten aufweist.
Einfach gesagt bilden sich in einem abgeschlossenen mechanischen System
(z. B. eine auf 2 Seiten eingespannte Saite, eine Luftsäule in einem Rohr, ein
geometrischer Gegenstand, eine Wasseroberfläche in einem Gefäß, etc.) bei
einer äußeren Anregung (z. B. Anzupfen, Anblasen, Anstreichen, Anschlagen)
nach einer Anschwingphase immer stehende Wellen aus, die durch
Überlagerung der an den Grenzen reflektierten Wellen entstehen.
Die Grundschwingung bei einer Saite wäre eine solche stehende Welle und
die höheren Harmonischen wären stehende Wellen mit einem oder mehreren Knoten.
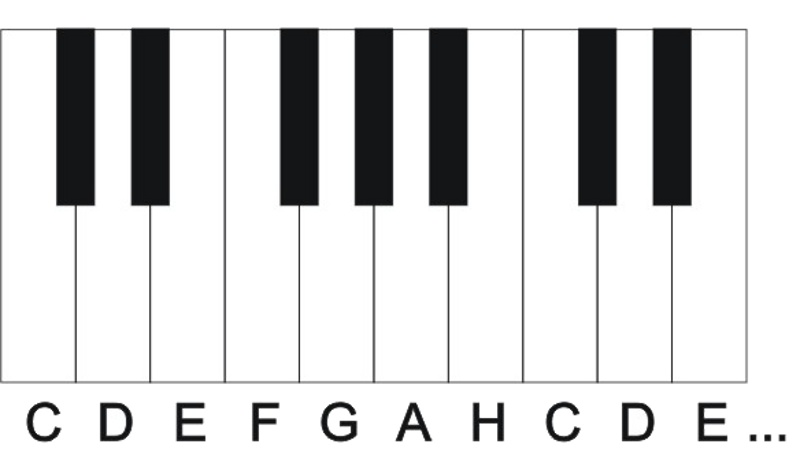
Der Bereich innerhalb eineer Oktave wird in der Musik in weitere Töne eingeteilt.
C, D, E, F, G, A, H, C (eine Oktave höher), D, E, usw.
In der westlichen Musik enthält jede Oktave 7 Ganztöne (weiße Klaviertasten) und mit dem 8. beginnt die nächste Oktave.
Jede Oktave enthält zusammen mit den Halbtönen (schwarze Klaviertasten) 12 Töne und mit dem 13. Ton beginnt die nächste Oktave.
Warum ist diese Einteilung der Oktave so, wie sie ist?
Im Dunklen Zeitalter sollten wir immer das Bekannteste und Alltäglichste sehr gut
hinterfragen: Stimmt das denn, wie es ist? Oder ist es anders?
Was könnte falsch sein an der allgegenwärtigen Instrumentenstimmung?
Die allgegenwärtige Stimmung in den Medien der westlichen Welt liegt bei einer Frequenz von 440 Hz für den Kammer-Ton A.
In den meisten Fällen wird eine gleichstufig temperierte Stimmung verwendet, bei der die Töne im Frequenzverhältnis exakt gleich verteilt sind.
Dies wird von den meisten als gegeben hingenommen. Es wird kaum hinterfragt, ob es auch andere Stimmungen gibt oder erspürt, wie die Wirkung dieser Stimmung ist.
Die gleichstufig temperierte Stimmung ist ein künstliches Konstrukt. Aus ihr entsteht ein exakt runder Quintenzirkel.
In der gleichstufig temperierten Stimmung lassen sich alle Tonarten gleichermaßen spielen.
Jedoch ist die Harmonie nicht exakt, weil die Quinten und Quarten nicht genau passen.
Gleichstufig temperierte Stimmung mit A auf 440 Hz (hier spielen)
| Ton | Frequenz | Primfaktoren | Frequenz- | Frequenz- | Frequenz- | Frequenz- | Quarten | Quinten |
| [Hz] | Verhältnis | Verhältnis | Verhältnis | Verhältnis | Rein = 4 / 3 | Rein = 3 / 2 | ||
| Ton (n+1)/n | zum C | zum C | zum C | = 1,333... | = 1,500... | |||
| Dezimal | Bruch | Dezimal | LOG2 | |||||
| C | 130,812783 | 1,059463 | 12.Wurzel(2^-12) | 0,500000 | -1,000000 | 1,334840 | 1,498307 | |
| C# / Db | 138,591315 | 1,059463 | 12.Wurzel(2^-11) | 0,529732 | -0,916667 | 1,334840 | 1,498307 | |
| D | 146,832384 | 1,059463 | 12.Wurzel(2^-10) | 0,561231 | -0,833333 | 1,334840 | 1,498307 | |
| D# / Eb | 155,563492 | 1,059463 | 12.Wurzel(2^-9) | 0,594604 | -0,750000 | 1,334840 | 1,498307 | |
| E | 164,813778 | 1,059463 | 12.Wurzel(2^-8) | 0,629961 | -0,666667 | 1,334840 | 1,498307 | |
| F | 174,614116 | 1,059463 | 12.Wurzel(2^-7) | 0,667420 | -0,583333 | 1,334840 | 1,498307 | |
| F# / Gb | 184,997211 | 1,059463 | 12.Wurzel(2^-6) | 0,707107 | -0,500000 | 1,334840 | 1,498307 | |
| G | 195,997718 | 1,059463 | 12.Wurzel(2^-5) | 0,749154 | -0,416667 | 1,334840 | 1,498307 | |
| G# / Ab | 207,652349 | 1,059463 | 12.Wurzel(2^-4) | 0,793701 | -0,333333 | 1,334840 | 1,498307 | |
| A | 220,000000 | 2*2*5*11 | 1,059463 | 12.Wurzel(2^-3) | 0,840896 | -0,250000 | 1,334840 | 1,498307 |
| A# / Bb | 233,081881 | 1,059463 | 12.Wurzel(2^-2) | 0,890899 | -0,166667 | 1,334840 | 1,498307 | |
| B | 246,941651 | 1,059463 | 12.Wurzel(2^-1) | 0,943874 | -0,083333 | 1,334840 | 1,498307 | |
| C | 261,625565 | 1,059463 | 12.Wurzel(2^0) | 1,000000 | 0,000000 | 1,334840 | 1,498307 | |
| C# / Db | 277,182631 | 1,059463 | 12.Wurzel(2^1) | 1,059463 | 0,083333 | 1,334840 | 1,498307 | |
| D | 293,664768 | 1,059463 | 12.Wurzel(2^2) | 1,122462 | 0,166667 | 1,334840 | 1,498307 | |
| D# / Eb | 311,126984 | 1,059463 | 12.Wurzel(2^3) | 1,189207 | 0,250000 | 1,334840 | 1,498307 | |
| E | 329,627557 | 1,059463 | 12.Wurzel(2^4) | 1,259921 | 0,333333 | 1,334840 | 1,498307 | |
| F | 349,228231 | 1,059463 | 12.Wurzel(2^5) | 1,334840 | 0,416667 | 1,334840 | 1,498307 | |
| F# / Gb | 369,994423 | 1,059463 | 12.Wurzel(2^6) | 1,414214 | 0,500000 | 1,334840 | 1,498307 | |
| G | 391,995436 | 1,059463 | 12.Wurzel(2^7) | 1,498307 | 0,583333 | 1,334840 | 1,498307 | |
| G# / Ab | 415,304698 | 1,059463 | 12.Wurzel(2^8) | 1,587401 | 0,666667 | 1,334840 | 1,498307 | |
| A | 440,000000 | 2*2*2*5*11 | 1,059463 | 12.Wurzel(2^9) | 1,681793 | 0,750000 | 1,334840 | 1,498307 |
| A# / Bb | 466,163762 | 1,059463 | 12.Wurzel(2^10) | 1,781797 | 0,833333 | 1,334840 | 1,498307 | |
| B | 493,883301 | 1,059463 | 12.Wurzel(2^11) | 1,887749 | 0,916667 | 1,334840 | 1,498307 | |
| C | 523,251131 | 1,059463 | 12.Wurzel(2^12) | 2,000000 | 1,000000 | 1,334840 | 1,498307 |
Merkmale:
- C nicht auf 256 Hz, A nicht auf 432 Hz, keine "heiligen" Zahlen bei den Frequenzen
- kein Ton ist aus Primfaktoren von 2 und 3 ableitbar
- exakte Spiegelung aller Töne beim LOG2-Frequenzverhältnis
- keine reinen Quarten
- keine reinen Quinten
- keine exakten Obertonüberlagerungen und damit keine exakte Harmonie
Es gibt auch alternative Stimmungen auf andere Frequenzen für den Kammer-Ton A.
Häufig wird eine Stimmung mit 432Hz für den Ton A empfohlen, da diese natürlicher und harmonischer wirken soll.
Schauen wir uns das einmal an:
Gleichstufig temperierte Stimmung mit A auf 432 Hz (hier spielen)
| Ton | Frequenz | Primfaktoren | Frequenz- | Frequenz- | Frequenz- | Frequenz- | Quarten | Quinten |
| [Hz] | Verhältnis | Verhältnis | Verhältnis | Verhältnis | Rein = 4 / 3 | Rein = 3 / 2 | ||
| Ton (n+1)/n | zum C | zum C | zum C | = 1,333... | = 1,500... | |||
| Dezimal | Bruch | Dezimal | LOG2 | |||||
| C | 128,434368 | 1,059463 | 12.Wurzel(2^-12) | 0,500000 | -1,000000 | 1,334840 | 1,498307 | |
| C# / Db | 136,071473 | 1,059463 | 12.Wurzel(2^-11) | 0,529732 | -0,916667 | 1,334840 | 1,498307 | |
| D | 144,162704 | 1,059463 | 12.Wurzel(2^-10) | 0,561231 | -0,833333 | 1,334840 | 1,498307 | |
| D# / Eb | 152,735065 | 1,059463 | 12.Wurzel(2^-9) | 0,594604 | -0,750000 | 1,334840 | 1,498307 | |
| E | 161,817164 | 1,059463 | 12.Wurzel(2^-8) | 0,629961 | -0,666667 | 1,334840 | 1,498307 | |
| F | 171,439314 | 1,059463 | 12.Wurzel(2^-7) | 0,667420 | -0,583333 | 1,334840 | 1,498307 | |
| F# / Gb | 181,633626 | 1,059463 | 12.Wurzel(2^-6) | 0,707107 | -0,500000 | 1,334840 | 1,498307 | |
| G | 192,434123 | 1,059463 | 12.Wurzel(2^-5) | 0,749154 | -0,416667 | 1,334840 | 1,498307 | |
| G# / Ab | 203,876852 | 1,059463 | 12.Wurzel(2^-4) | 0,793701 | -0,333333 | 1,334840 | 1,498307 | |
| A | 216,000000 | 2*2*2*3*3*3 | 1,059463 | 12.Wurzel(2^-3) | 0,840896 | -0,250000 | 1,334840 | 1,498307 |
| A# / Bb | 228,844028 | 1,059463 | 12.Wurzel(2^-2) | 0,890899 | -0,166667 | 1,334840 | 1,498307 | |
| B | 242,451802 | 1,059463 | 12.Wurzel(2^-1) | 0,943874 | -0,083333 | 1,334840 | 1,498307 | |
| C | 256,868737 | 1,059463 | 12.Wurzel(2^0) | 1,000000 | 0,000000 | 1,334840 | 1,498307 | |
| C# / Db | 272,142947 | 1,059463 | 12.Wurzel(2^1) | 1,059463 | 0,083333 | 1,334840 | 1,498307 | |
| D | 288,325409 | 1,059463 | 12.Wurzel(2^2) | 1,122462 | 0,166667 | 1,334840 | 1,498307 | |
| D# / Eb | 305,470129 | 1,059463 | 12.Wurzel(2^3) | 1,189207 | 0,250000 | 1,334840 | 1,498307 | |
| E | 323,634329 | 1,059463 | 12.Wurzel(2^4) | 1,259921 | 0,333333 | 1,334840 | 1,498307 | |
| F | 342,878627 | 1,059463 | 12.Wurzel(2^5) | 1,334840 | 0,416667 | 1,334840 | 1,498307 | |
| F# / Gb | 363,267251 | 1,059463 | 12.Wurzel(2^6) | 1,414214 | 0,500000 | 1,334840 | 1,498307 | |
| G | 384,868246 | 1,059463 | 12.Wurzel(2^7) | 1,498307 | 0,583333 | 1,334840 | 1,498307 | |
| G# / Ab | 407,753703 | 1,059463 | 12.Wurzel(2^8) | 1,587401 | 0,666667 | 1,334840 | 1,498307 | |
| A | 432,000000 | 2*2*2*2*3*3*3 | 1,059463 | 12.Wurzel(2^9) | 1,681793 | 0,750000 | 1,334840 | 1,498307 |
| A# / Bb | 457,688057 | 1,059463 | 12.Wurzel(2^10) | 1,781797 | 0,833333 | 1,334840 | 1,498307 | |
| B | 484,903605 | 1,059463 | 12.Wurzel(2^11) | 1,887749 | 0,916667 | 1,334840 | 1,498307 | |
| C | 513,737474 | 1,059463 | 12.Wurzel(2^12) | 2,000000 | 1,000000 | 1,334840 | 1,498307 |
Merkmale:
- C nicht auf 256 Hz, wenn A auf 432 Hz, bis auf das A keine "heiligen" Zahlen bei den Frequenzen
- nur der Ton A ist aus Primfaktoren von 2 und 3 ableitbar
- exakte Spiegelung aller Töne beim LOG2-Frequenzverhältnis
- keine reinen Quarten
- keine reinen Quinten
- keine exakten Obertonüberlagerungen und damit keine exakte Harmonie
Gleichstufig temperierte Stimmung mit C auf 256 Hz (hier spielen)
| Ton | Frequenz | Primfaktoren | Frequenz- | Frequenz- | Frequenz- | Frequenz- | Quarten | Quinten |
| [Hz] | Verhältnis | Verhältnis | Verhältnis | Verhältnis | Rein = 4 / 3 | Rein = 3 / 2 | ||
| Ton (n+1)/n | zum C 256 | zum C 256 | zum C 256 | = 1,333... | = 1,500... | |||
| Dezimal | Bruch | Dezimal | LOG2 | |||||
| C | 128,000000 | 2*2*2*2*2*2*2 | 1,059463 | 12.Wurzel(2^-12) | 0,500000 | -1,000000 | 1,334840 | 1,498307 |
| C# / Db | 135,611276 | 1,059463 | 12.Wurzel(2^-11) | 0,529732 | -0,916667 | 1,334840 | 1,498307 | |
| D | 143,675142 | 1,059463 | 12.Wurzel(2^-10) | 0,561231 | -0,833333 | 1,334840 | 1,498307 | |
| D# / Eb | 152,218511 | 1,059463 | 12.Wurzel(2^-9) | 0,594604 | -0,750000 | 1,334840 | 1,498307 | |
| E | 161,269894 | 1,059463 | 12.Wurzel(2^-8) | 0,629961 | -0,666667 | 1,334840 | 1,498307 | |
| F | 170,859501 | 1,059463 | 12.Wurzel(2^-7) | 0,667420 | -0,583333 | 1,334840 | 1,498307 | |
| F# / Gb | 181,019336 | 1,059463 | 12.Wurzel(2^-6) | 0,707107 | -0,500000 | 1,334840 | 1,498307 | |
| G | 191,783306 | 1,059463 | 12.Wurzel(2^-5) | 0,749154 | -0,416667 | 1,334840 | 1,498307 | |
| G# / Ab | 203,187335 | 1,059463 | 12.Wurzel(2^-4) | 0,793701 | -0,333333 | 1,334840 | 1,498307 | |
| A | 215,269482 | 1,059463 | 12.Wurzel(2^-3) | 0,840896 | -0,250000 | 1,334840 | 1,498307 | |
| A# / Bb | 228,070072 | 1,059463 | 12.Wurzel(2^-2) | 0,890899 | -0,166667 | 1,334840 | 1,498307 | |
| B | 241,631824 | 1,059463 | 12.Wurzel(2^-1) | 0,943874 | -0,083333 | 1,334840 | 1,498307 | |
| C | 256,000000 | 2*2*2*2*2*2*2*2 | 1,059463 | 12.Wurzel(2^0) | 1,000000 | 0,000000 | 1,334840 | 1,498307 |
| C# / Db | 271,222552 | 1,059463 | 12.Wurzel(2^1) | 1,059463 | 0,083333 | 1,334840 | 1,498307 | |
| D | 287,350284 | 1,059463 | 12.Wurzel(2^2) | 1,122462 | 0,166667 | 1,334840 | 1,498307 | |
| D# / Eb | 304,437021 | 1,059463 | 12.Wurzel(2^3) | 1,189207 | 0,250000 | 1,334840 | 1,498307 | |
| E | 322,539789 | 1,059463 | 12.Wurzel(2^4) | 1,259921 | 0,333333 | 1,334840 | 1,498307 | |
| F | 341,719003 | 1,059463 | 12.Wurzel(2^5) | 1,334840 | 0,416667 | 1,334840 | 1,498307 | |
| F# / Gb | 362,038672 | 1,059463 | 12.Wurzel(2^6) | 1,414214 | 0,500000 | 1,334840 | 1,498307 | |
| G | 383,566612 | 1,059463 | 12.Wurzel(2^7) | 1,498307 | 0,583333 | 1,334840 | 1,498307 | |
| G# / Ab | 406,374669 | 1,059463 | 12.Wurzel(2^8) | 1,587401 | 0,666667 | 1,334840 | 1,498307 | |
| A | 430,538965 | 1,059463 | 12.Wurzel(2^9) | 1,681793 | 0,750000 | 1,334840 | 1,498307 | |
| A# / Bb | 456,140144 | 1,059463 | 12.Wurzel(2^10) | 1,781797 | 0,833333 | 1,334840 | 1,498307 | |
| B | 483,263648 | 1,059463 | 12.Wurzel(2^11) | 1,887749 | 0,916667 | 1,334840 | 1,498307 | |
| C | 512,000000 | 2*2*2*2*2*2*2*2*2 | 1,059463 | 12.Wurzel(2^12) | 2,000000 | 1,000000 | 1,334840 | 1,498307 |
Merkmale:
- A nicht auf 432 Hz, wenn C auf 256 Hz, bis auf das C keine "heiligen" Zahlen bei den Frequenzen
- nur der Ton C ist aus Primfaktoren von 2 ableitbar
- exakte Spiegelung aller Töne beim LOG2-Frequenzverhältnis
- keine reinen Quarten
- keine reinen Quinten
- keine exakten Obertonüberlagerungen und damit keine exakte Harmonie
Eine Stimmung auf den Kammer-Ton A mit 432Hz oder ein C mit 256 Hz ist noch
nicht automatisch harmonisch, wenn eine gleichstufig temperierte Stimmung beibehalten wird!
Es reicht nicht, wenn nur ein Ton der Tonleiter harmonischer oder natürlicher ist.
Alle Töne und deren Frequenzverhältnisse müssen miteinander passen, damit exakte Harmonie entsteht.
In allen Schöpfungen des Lebens spielen immer bestimmte Zahlen, Muster und Gesetze eine Rolle.
Was ist überhaupt Harmonie?
Jeder natürliche Ton hat immer eine Grundfrequenz (1x) und Obertöne mit den Vielfachen (2x, 3x, 4x, usw.) dieser Frequenz.
In der Schöpfung beginnt alles mit der Zahl 1 - also sollten wir den ersten Ton ebenfalls mit 1 Hz wählen,
was genau einer Schwingung in einer Sekunde entspricht - also beispielsweise wenn eine gespannte Saite schwingt.
Ein Ton mit der Grundfrequenz von 1 Hz bildet Oberwellen mit 2 Hz, 3 Hz, 4 Hz, usw.
Die Oktaven von 1 Hz ergeben sich, wenn wir die Länge der Saite immer wieder halbieren.
Länge 1 = 1 Hz
Länge 1/2 = 2 Hz
Länge 1/4 = 4 Hz
Länge 1/8 = 8 Hz
usw.
Diesen Ton mit 1 Hz bezeichnen wir als Grundton. Im westlichen Musik-System wird er mit dem Buchstaben C notiert.
Oktav-Frequenzen: 1 Hz, 2 Hz, 4 Hz, 8 Hz, 16 Hz, 32 Hz, 64 Hz, 128 Hz, 256 Hz, 512 Hz, 1024 Hz, 2048 Hz, 4096 Hz, usw.
Die Grundfrequenz der Schumann-Resonanz der Erde liegt nahe bei 8 Hz - Diese Frequenz finden wir auch in den Biorhythmen und Nervensystemen
der Lebewesen. Eine Stimmung auf 8 Hz und deren Vielfachen soll sehr Harmonisch auf unser Bewusstsein, das Herz und das Gehirn wirken.
Damit in der Musik Harmonie entsteht, müssen immer 2 Töne vorhanden sein, die miteinander in Einklang sind.
Je mehr Obertöne sich bei 2 Tönen überlagern, desto größer ist die empfundene Harmonie (Einklang).
Die einfachste Harmonie entsteht, wenn 2 Töne mit der gleichen Frequenz gleichzeitig erklingen.
Dann liegen alle Obertöne exakt übereinander und es entsteht maximale Harmonie (Einklang).
Die Grundtöne mit 256 Hz stehen im Verhältnis 1 / 1.
| Ton | Verhältnis | Frequenz | 2x | 3x | 4x | 5x | 6x | 7x | 8x | 9x | 10x | 11x | 12x |
| 1 | 1 | 256 | 512 | 768 | 1024 | 1280 | 1536 | 1792 | 2048 | 2304 | 2560 | 2816 | 3072 |
| 2 | 1 | 256 | 512 | 768 | 1024 | 1280 | 1536 | 1792 | 2048 | 2304 | 2560 | 2816 | 3072 |
Wenn wir einen Grundton gemeinsam mit einem Ton seiner Oktav-Frequenzen spielen,
z. B. 256 Hz und 512 Hz --> dann ergeben sich bei den Obertönen ebenfalls gemeinsame Frequenzen, die für unser Ohr gut klingen.
Diese Grundtöne stehen im Verhältnis 1 / 2 bzw. 2 / 1.
| Ton | Verhältnis | Frequenz | 2x | 3x | 4x | 5x | 6x | 7x | 8x | 9x | 10x | 11x | 12x |
| 1 | 1 | 256 | 512 | 768 | 1024 | 1280 | 1536 | 1792 | 2048 | 2304 | 2560 | 2816 | 3072 |
| 2 | 2 | 512 | 1024 | 1536 | 2048 | 2560 | 3072 | 3584 | 4096 | 4608 | 5120 | 5632 | 6144 |
Wie entstehen nun die anderen Töne in der Tonleiter?
Indem wir weitere Harmonien finden.
Harmonische Töne entstehen immer dann, wenn deren Frequenzen (Grundton und Obertäne) in einem Verhältnis von ganzen Zahlen zueinander stehen.
Sehen wir also, welches Verhältnis das nächste sein könnte:
Grundtöne im Verhältnis 1 / 3 bzw. 3 / 1 --> auch hier ergeben sich bei den Obertönen gemeinsame Frequenzen, die für unser Ohr gut klingen.
Aber das Verhältnis dieser Töne ist schon größer als eine Oktave (Verhältnis 2 / 1), deshalb ist es ungeeignet für eine Tonleiter zwischen zwei Oktav-Frequenzen (1 /1 bis 2 / 1).
In dieser Tonleiter müssen alle Zwischentöne im Bereich von 1 / 1 bis 2 / 1 liegen, also im Beispiel zwischen 256 Hz und 512 Hz.
| Ton | Verhältnis | Frequenz | 2x | 3x | 4x | 5x | 6x | 7x | 8x | 9x | 10x | 11x | 12x |
| 1 | 1 | 256 | 512 | 768 | 1024 | 1280 | 1536 | 1792 | 2048 | 2304 | 2560 | 2816 | 3072 |
| 2 | 3 | 768 | 1536 | 2304 | 3072 | 3840 | 4608 | 5376 | 6144 | 6912 | 7680 | 8448 | 9216 |
Grundtöne im Verhältnis 2 / 3 bzw. 3 / 2 --> auch hier ergeben sich bei den Obertönen gemeinsame Frequenzen, die für unser Ohr gut klingen.
Dieses Verhältnis der Frequenzen wird im westlichen System als reine Quinte bezeichnet und klingt sehr harmonisch (z. B. Ton C und G gemeinsam gespielt).
| Ton | Verhältnis | Frequenz | 2x | 3x | 4x | 5x | 6x | 7x | 8x | 9x | 10x | 11x | 12x |
| 1 | 2 | 256 | 512 | 768 | 1024 | 1280 | 1536 | 1792 | 2048 | 2304 | 2560 | 2816 | 3072 |
| 2 | 3 | 384 | 768 | 1152 | 1536 | 1920 | 2304 | 2688 | 3072 | 3456 | 3840 | 4224 | 4608 |
Grundtöne im Verhältnis 3 / 4 bzw. 4 / 3 --> auch hier wieder Obertöne mit gemeinsamen Frequenzen
Dieses Verhältnis der Frequenzen wird im westlichen System als reine Quarte bezeichnet und klingt auch harmonisch (z. B. Ton C und F gemeinsam gespielt).
| Ton | Verhältnis | Frequenz | 2x | 3x | 4x | 5x | 6x | 7x | 8x | 9x | 10x | 11x | 12x |
| 1 | 3 |
256,00 | 512,00 | 768,00 | 1024,00 | 1280,00 | 1536,00 | 1792,00 | 2048,00 | 2304,00 | 2560,00 | 2816,00 | 3072,00 |
| 2 | 4 |
341,33 | 682,67 | 1024,00 | 1365,33 | 1706,67 | 2048,00 | 2389,33 | 2730,67 | 3072,00 | 3413,33 | 3754,67 | 4096,00 |
Die folgende Grafik zeigt den Grundton und dessen Obertöne auf dem mittleren Strahl. Darüber und darunter sind die Quarten, Quinten und Oktaven mit ihren Obertönen.
Je mehr Obertöne von der Frequenz genau übereinander liegen (siehe graue Hilfslinien), desto harmonischer empfinden wir 2 gemeinsam klingende Töne.

Die anderen Töne der Tonleiter möchte ich nun auf einem besonderen Weg herleiten:
Die Primzahlen sind nur durch sich selbst und durch 1 teilbar:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, ...
Die Primzahl 2 haben wir verwendet, als wir die Oktaven von einem Grundton mit 1 Hz gebildet haben.
Oktav-Frequenzen: 1 Hz, 2 Hz, 4 Hz, 8 Hz, 16 Hz, 32 Hz, 64 Hz, 128 Hz, 256 Hz, 512 Hz, 1024 Hz, 2048 Hz, 4096 Hz, usw.
Hier wurde für den nächst höheren Oktav-Ton die Frequenz jeweils verdoppelt.
Die Primzahl 3 ist die nächste, die wir nun genauer ansehen wollen:
Frequenzen: 1 Hz, 3 Hz, 9 Hz, 27 Hz, 81 Hz, 243 Hz, 729 Hz, 2187 Hz, 6561 Hz, usw.
Hier erhalten wir die nächste Frequenz immer über eine Verdreifachung.
In der folgenden Tabelle wurden die Zahlen nach unten verdoppelt und nach rechts verdreifacht:
| 1 | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 |
| 2 | 6 | 18 | 54 | 162 | 486 | 1458 | 4374 | 13122 |
| 4 | 12 | 36 | 108 | 324 | 972 | 2916 | 8748 | 26244 |
| 8 | 24 | 72 | 216 | 648 | 1944 | 5832 | 17496 | 52488 |
| 16 | 48 | 144 | 432 | 1296 | 3888 | 11664 | 34992 | 104976 |
| 32 | 96 | 288 | 864 | 2592 | 7776 | 23328 | 69984 | 209952 |
| 64 | 192 | 576 | 1728 | 5184 | 15552 | 46656 | 139968 | 419904 |
| 128 | 384 | 1152 | 3456 | 10368 | 31104 | 93312 | 279936 | 839808 |
| 256 | 768 | 2304 | 6912 | 20736 | 62208 | 186624 | 559872 | 1679616 |
| 512 | 1536 | 4608 | 13824 | 41472 | 124416 | 373248 | 1119744 | 3359232 |
| 1024 | 3072 | 9216 | 27648 | 82944 | 248832 | 746496 | 2239488 | 6718464 |
| 2048 | 6144 | 18432 | 55296 | 165888 | 497664 | 1492992 | 4478976 | 13436928 |
| 4096 | 12288 | 36864 | 110592 | 331776 | 995328 | 2985984 | 8957952 | 26873856 |
Hier sehen wir einige Zahlen, die in vielen Kulturen oder auch Religionen der Welt eine wichtige Rolle spielen:
1, 2, 3, 4, 6, 8, 9, 12, 16, 36, 64, 72, 81, 108, 144, uvm.
3 Einigkeit, 12 Monate, 2 mal 12 Stunden auf der Uhr, 360° im Kreis, 108 Perlen an Gebetsketten, usw.
Es sind "heilige" Zahlen, die in der Schöpfung eine große Rolle spielen und auch in der Heiligen Geometrie sehr wichtig sind.
Nun geht es weiter mit der Herleitung einer harmonischen Tonleiter:
Die Oktave mit dem Frequenz-Verhältnis 2 / 1 und die Quinte mit dem Frequenz-Verhältnis 3 / 2 haben wir als sehr harmonisch erkannt.
Nun verwenden wir diese für die Herleitung der anderen Töne der Tonleiter.
Eine Oktave kommt von okta = 8. = der achte Ton
Der 1. Ton ist ein C, der 8. ganze Ton nach dem C ist wieder ein C, nur eine Oktave höher.
Quinte kommt von quinta = 5. = der fünfte Ton
Der 1. Ton ist ein C, der 5. ganze Ton nach dem C ist ein G. Das C und G bilden eine Quinte.
Oktaven und Quinten
In folgender Tabelle sind in der Mitte der Grundton C und seine Oktav-Frequenzen nach unten aufgetragen.
Eine Zeile nach unten wird die Frequenz um 2 / 1 größer - eine Oktave höher. Eine Zeile nach oben wird die Frequenz um 1 / 2 kleiner - eine Oktave niedriger.
Eine Spalte nach links wird die Frequenz immer um 2 / 3 kleiner - eine Quinte niedriger. Eine Spalte nach rechts wird die Frequenz immer um 3 / 2 größer - eine Quinte höher.
| B* | F#/Gb* | C#/Db | G#/Ab | D#/Eb | A#/Bb | F | C | G | D | A | E | B | F#/Gb | C#/Db* |
| 0,059 | 0,088 | 0,132 | 0,198 | 0,296 | 0,444 | 0,667 | 1 | 1,5 | 2,25 | 3,375 | 5,0625 | 7,59375 | 11,390625 | 17,0859375 |
| 0,117 | 0,176 | 0,263 | 0,395 | 0,593 | 0,889 | 1,333 | 2 | 3 | 4,5 | 6,75 | 10,125 | 15,1875 | 22,78125 | 34,171875 |
| 0,234 | 0,351 | 0,527 | 0,790 | 1,185 | 1,778 | 2,667 | 4 | 6 | 9 | 13,5 | 20,25 | 30,375 | 45,5625 | 68,34375 |
| 0,468 | 0,702 | 1,053 | 1,580 | 2,370 | 3,556 | 5,333 | 8 | 12 | 18 | 27 | 40,5 | 60,75 | 91,125 | 136,6875 |
| 0,936 | 1,405 | 2,107 | 3,160 | 4,741 | 7,111 | 10,667 | 16 | 24 | 36 | 54 | 81 | 121,5 | 182,25 | 273,375 |
| 1,873 | 2,809 | 4,214 | 6,321 | 9,481 | 14,222 | 21,333 | 32 | 48 | 72 | 108 | 162 | 243 | 364,5 | 546,75 |
| 3,746 | 5,619 | 8,428 | 12,642 | 18,963 | 28,444 | 42,667 | 64 | 96 | 144 | 216 | 324 | 486 | 729 | 1093,5 |
| 7,492 | 11,237 | 16,856 | 25,284 | 37,926 | 56,889 | 85,333 | 128 | 192 | 288 | 432 | 648 | 972 | 1458 | 2187 |
| 14,983 | 22,475 | 33,712 | 50,568 | 75,852 | 113,778 | 170,667 | 256 | 384 | 576 | 864 | 1296 | 1944 | 2916 | 4374 |
| 29,966 | 44,949 | 67,424 | 101,136 | 151,704 | 227,556 | 341,333 | 512 | 768 | 1152 | 1728 | 2592 | 3888 | 5832 | 8748 |
| 59,932 | 89,898 | 134,848 | 202,272 | 303,407 | 455,111 | 682,667 | 1024 | 1536 | 2304 | 3456 | 5184 | 7776 | 11664 | 17496 |
| 119,865 | 179,797 | 269,695 | 404,543 | 606,815 | 910,222 | 1365,333 | 2048 | 3072 | 4608 | 6912 | 10368 | 15552 | 23328 | 34992 |
| 239,729 | 359,594 | 539,391 | 809,086 | 1213,630 | 1820,444 | 2730,667 | 4096 | 6144 | 9216 | 13824 | 20736 | 31104 | 46656 | 69984 |
| 479,459 | 719,188 | 1078,782 | 1618,173 | 2427,259 | 3640,889 | 5461,333 | 8192 | 12288 | 18432 | 27648 | 41472 | 62208 | 93312 | 139968 |
| 958,917 | 1438,376 | 2157,564 | 3236,346 | 4854,519 | 7281,778 | 10922,667 | 16384 | 24576 | 36864 | 55296 | 82944 | 124416 | 186624 | 279936 |
| 1917,834 | 2876,752 | 4315,128 | 6472,691 | 9709,037 | 14563,556 | 21845,333 | 32768 | 49152 | 73728 | 110592 | 165888 | 248832 | 373248 | 559872 |
So entsteht auch der Quintenzirkel, der in der Musik und Harmonielehre eine große Rolle spielt.
Hinweis: Mit reinen Quinten ergibt sich kein Quintenzirkel, sondern genauer eine Quintenspirale!
Bei der Quintenspirale liegt die Frequenz von einem Ton nach einem Umlauf etwas höher.
Die Abweichung nach einer Runde (Verhältnis vom 13. zum 1. Ton): z. B. von F#/Gb* zu F#/Gb = 364,5 / 359,594 = 1,013643…
Dieses Verhältnis ist das Pythagoräische Komma: 3^12 / 2^19 = 1,0136432647705078125 …
Von einem beliebigen Ton ausgehend, 12 reine Quinten aufwärts und dann 7 Oktaven abwärts, gelangen wir nicht zum Ausgangston, sondern zu einem um diesem Faktor höheren Ton!
Wegen diesem von 1 abweichenden Faktor lässt sich die Tonleiter (aus reinen Quinten hergeleitet) nicht exakt zyklisch schließen!
Der Quintenzirkel und die gleichstufig temperierte Stimmung sind künstliche Konstrukte, wobei die Spirale in einen Kreis mit exakt gleichen Tonabständen gezwungen wurde.
Die reinen Quinten und die exakte Obertonharmonie gehen dabei verloren. Dafür lassen sich dann alle Tonarten gleichermaßen spielen und ineinander transponieren.
Oktaven und Quarten
Quarte kommt von quarta = 4. = der vierte Ton
Der 1. Ton ist ein C, der 4. ganze Ton nach dem C ist ein F. Das C und F bilden eine Quarte.
In folgender Tabelle sind in der Mitte der Grundton C und seine Oktav-Frequenzen nach unten aufgetragen.
Eine Zeile nach unten wird die Frequenz um 2 / 1 größer - eine Oktave höher. Eine Zeile nach oben wird die Frequenz um 1 / 2 kleiner - eine Oktave niedriger.
Eine Spalte nach links wird die Frequenz immer um 3 / 4 kleiner - eine Quarte niedriger. Eine Spalte nach rechts wird die Frequenz immer um 4 / 3 größer - eine Quarte höher.
| C#/Db* | F#/Gb | B | E | A | D | G | C | F | A#/Bb | D#/Eb | G#/Ab | C#/Db | F#/Gb* | B* |
| 0,1334838867 | 0,1779785156 | 0,2373046875 | 0,31640625 | 0,421875 | 0,5625 | 0,75 | 1 | 1,333 | 1,778 | 2,370 | 3,160 | 4,214 | 5,619 | 7,492 |
| 0,2669677734 | 0,3559570313 | 0,474609375 | 0,6328125 | 0,84375 | 1,125 | 1,5 | 2 | 2,667 | 3,556 | 4,741 | 6,321 | 8,428 | 11,237 | 14,983 |
| 0,5339355469 | 0,7119140625 | 0,94921875 | 1,265625 | 1,6875 | 2,25 | 3 | 4 | 5,333 | 7,111 | 9,481 | 12,642 | 16,856 | 22,475 | 29,966 |
| 1,0678710938 | 1,423828125 | 1,8984375 | 2,53125 | 3,375 | 4,5 | 6 | 8 | 10,667 | 14,222 | 18,963 | 25,284 | 33,712 | 44,949 | 59,932 |
| 2,1357421875 | 2,84765625 | 3,796875 | 5,0625 | 6,75 | 9 | 12 | 16 | 21,333 | 28,444 | 37,926 | 50,568 | 67,424 | 89,898 | 119,865 |
| 4,271484375 | 5,6953125 | 7,59375 | 10,125 | 13,5 | 18 | 24 | 32 | 42,667 | 56,889 | 75,852 | 101,136 | 134,848 | 179,797 | 239,729 |
| 8,54296875 | 11,390625 | 15,1875 | 20,25 | 27 | 36 | 48 | 64 | 85,333 | 113,778 | 151,704 | 202,272 | 269,695 | 359,594 | 479,459 |
| 17,0859375 | 22,78125 | 30,375 | 40,5 | 54 | 72 | 96 | 128 | 170,667 | 227,556 | 303,407 | 404,543 | 539,391 | 719,188 | 958,917 |
| 34,171875 | 45,5625 | 60,75 | 81 | 108 | 144 | 192 | 256 | 341,333 | 455,111 | 606,815 | 809,086 | 1078,782 | 1438,376 | 1917,834 |
| 68,34375 | 91,125 | 121,5 | 162 | 216 | 288 | 384 | 512 | 682,667 | 910,222 | 1213,630 | 1618,173 | 2157,564 | 2876,752 | 3835,669 |
| 136,6875 | 182,25 | 243 | 324 | 432 | 576 | 768 | 1024 | 1365,333 | 1820,444 | 2427,259 | 3236,346 | 4315,128 | 5753,503 | 7671,338 |
| 273,375 | 364,5 | 486 | 648 | 864 | 1152 | 1536 | 2048 | 2730,667 | 3640,889 | 4854,519 | 6472,691 | 8630,255 | 11507,007 | 15342,676 |
| 546,75 | 729 | 972 | 1296 | 1728 | 2304 | 3072 | 4096 | 5461,333 | 7281,778 | 9709,037 | 12945,383 | 17260,510 | 23014,014 | 30685,352 |
| 1093,5 | 1458 | 1944 | 2592 | 3456 | 4608 | 6144 | 8192 | 10922,667 | 14563,556 | 19418,074 | 25890,765 | 34521,021 | 46028,027 | 61370,703 |
| 2187 | 2916 | 3888 | 5184 | 6912 | 9216 | 12288 | 16384 | 21845,333 | 29127,111 | 38836,148 | 51781,531 | 69042,041 | 92056,055 | 122741,406 |
| 4374 | 5832 | 7776 | 10368 | 13824 | 18432 | 24576 | 32768 | 43690,667 | 58254,222 | 77672,296 | 103563,062 | 138084,082 | 184112,110 | 245482,813 |
Die Verdopplungs-Reihe wurde jeweils grün und die Verdreifachungs-Reihe jeweils blau markiert.
In der Herleitung sollen alle Töne der Tonleiter im Bereich von 1 / 1 bis 2 / 1 liegen, also im Beispiel zwischen
256 Hz und 512 Hz. Deshalb wurden in jeder Spalte die Töne in der passenden Oktave markiert.
Es könnte auch jede andere Oktave mit einem entsprechenden Frequenzbereich verwendet werden.
Ein Vergleich der beiden Tabellen zeigt, dass die Herleitung sowohl über die Quinte, als auch über die Quarte möglich sind.
Dies kann damit erklärt werden, dass Quinte und Quarte Komplementärintervalle sind. Komplementärintervalle
ergänzen sich und ergeben miteinander eine Oktave: z. B. Quinte C-G und Quarte G-C
oder Quarte C-F und Quinte F-C.
Die gleichen Töne und Frequenzen erscheinen in den obigen beiden Tabellen ("Oktaven und Quinten", "Oktaven und Quarten") jeweils links und rechts gespiegelt.
Als Ergebnis entsteht eine Tonleiter, die auf harmonischen Zahlen und Zahlenverhältnissen aufgebaut ist.
Diese wurde schon von den Pythagoräern (Schule des Pythagoras) entdeckt, die auch ein sehr großes Wissen in der Heiligen Geometrie hatten.
Harmonische Stimmung – Pythagoräische Scale (hier spielen)
| Ton | Frequenz | Primfaktoren | Frequenz- | Frequenz- | Frequenz- | Frequenz- | Quarten | Quinten |
| [Hz] | Verhältnis | Verhältnis | Verhältnis | Verhältnis | Rein = 4 / 3 | Rein = 3 / 2 | ||
| Ton (n+1)/n | zum C 256 | zum C 256 | zum C 256 | = 1,333... | = 1,500... | |||
| Dezimal | Bruch | Dezimal | LOG2 | |||||
| C | 128,000000 | 3⁰ * 2⁷ | 1,053498 | 1 / 2 | 0,500000 | -1,000000 | 1,333333 | 1,500000 |
| C# / Db | 134,847737 | 2¹⁵ / 3⁵ | 1,053498 | 128 / 243 | 0,526749 | -0,924813 | 1,333333 | 1,479811 |
| D | 144,000000 | 3² * 2⁴ | 1,067871 | 9 / 16 | 0,562500 | -0,830075 | 1,333333 | 1,500000 |
| D# / Eb | 151,703704 | 2¹² / 3³ | 1,053498 | 16 / 27 | 0,592593 | -0,754888 | 1,333333 | 1,500000 |
| E | 162,000000 | 3⁴ * 2¹ | 1,067871 | 81 / 128 | 0,632813 | -0,660150 | 1,333333 | 1,500000 |
| F | 170,666667 | 2⁹ / 3¹ | 1,053498 | 2 / 3 | 0,666667 | -0,584963 | 1,333333 | 1,500000 |
| F# / Gb | 182,250000 | 3⁶ / 2² | 1,067871 | 729/1024 | 0,711914 | -0,490225 | 1,351524 | 1,500000 |
| G | 192,000000 | 3¹ * 2⁶ | 1,053498 | 3 / 4 | 0,750000 | -0,415037 | 1,333333 | 1,500000 |
| G# / Ab | 202,271605 | 2¹⁴ / 3⁴ | 1,053498 | 64 / 81 | 0,790123 | -0,339850 | 1,333333 | 1,500000 |
| A | 216,000000 | 3³ * 2³ | 1,067871 | 27 / 32 | 0,843750 | -0,245112 | 1,333333 | 1,500000 |
| A# / Bb | 227,555556 | 2¹¹ / 3² | 1,053498 | 8 / 9 | 0,888889 | -0,169925 | 1,333333 | 1,500000 |
| B | 243,000000 | 3⁵ * 2⁰ | 1,067871 | 243 / 256 | 0,949219 | -0,075187 | 1,333333 | 1,500000 |
| C | 256,000000 | 3⁰ * 2⁸ | 1,053498 | 1 / 1 | 1,000000 | 0,000000 | 1,333333 | 1,500000 |
| C# / Db | 269,695473 | 2¹⁶ / 3⁵ | 1,053498 | 256 / 243 | 1,053498 | 0,075187 | 1,333333 | 1,479811 |
| D | 288,000000 | 3² * 2⁵ | 1,067871 | 9 / 8 | 1,125000 | 0,169925 | 1,333333 | 1,500000 |
| D# / Eb | 303,407407 | 2¹³ / 3³ | 1,053498 | 32 / 27 | 1,185185 | 0,245112 | 1,333333 | 1,500000 |
| E | 324,000000 | 3⁴ * 2² | 1,067871 | 81 / 64 | 1,265625 | 0,339850 | 1,333333 | 1,500000 |
| F | 341,333333 | 2¹⁰ / 3¹ | 1,053498 | 4 / 3 | 1,333333 | 0,415037 | 1,333333 | 1,500000 |
| F# / Gb | 364,500000 | 3⁶ / 2¹ | 1,067871 | 729 / 512 | 1,423828 | 0,509775 | 1,351524 | 1,500000 |
| G | 384,000000 | 3¹ * 2⁷ | 1,053498 | 3 / 2 | 1,500000 | 0,584963 | 1,333333 | 1,500000 |
| G# / Ab | 404,543210 | 2¹⁵ / 3⁴ | 1,053498 | 128 / 81 | 1,580247 | 0,660150 | 1,333333 | 1,500000 |
| A | 432,000000 | 3³ * 2⁴ | 1,067871 | 27 / 16 | 1,687500 | 0,754888 | 1,333333 | 1,500000 |
| A# / Bb | 455,111111 | 2¹² / 3² | 1,053498 | 16 / 9 | 1,777778 | 0,830075 | 1,333333 | 1,500000 |
| B | 486,000000 | 3⁵ * 2¹ | 1,067871 | 243 / 128 | 1,898438 | 0,924813 | 1,333333 | 1,500000 |
| C | 512,000000 | 3⁰ * 2⁹ | 1,053498 | 2 / 1 | 2,000000 | 1,000000 | 1,333333 | 1,500000 |
Merkmale:
- A auf 432 Hz, wenn C auf 256 Hz, viele "heilige" Zahlen bei den Frequenzen der Töne
- Töne C, G, D, A, E, B, F#/Gb sind aus dem Produkt der Primzahl-Potenzen von 2 (Oktaven-Sprung *2) und 3 (Quinten-Sprung *3/2) ableitbar 3^m*2^n
- Töne C#/Db, G#/Ab, D#/Eb, A#/Bb, F sind aus dem Quotient der Primzahlen-Potenzen von 2 (Oktaven-Sprung *2) und 3 (Quinten-Sprung*2/3) ableitbar 2^m/3^n
- bis auf den Ton F#/Gb exakte Spiegelung der Töne beim LOG2-Frequenzverhältnis
- 12 von 13 reine Quarten in der Oktave, 1 Quarte mit größerer Abweichung (als unharmonisch empfunden)
- 12 von 13 reine Quinten in der Oktave, 1 Quinte mit größerer Abweichung (als unharmonisch empfunden)
- viele exakte Obertonüberlagerungen (Quarten und Quinten) und damit viel Harmonie
Mathematische Auffälligkeiten:
Der Ton G liegt mit der Frequenz exakt in der Mitte zwischen den Tönen C einer Oktave (Quinte C-G und Quarte G-C)
arithmetischer Mittelwert: ( 256 Hz + 512 Hz ) / 2 = 768 Hz / 2 = 384 Hz
Die ganzzahligen Frequenzverhältnisse zum C 256 in obiger Tabelle spiegeln sich um das C mit 256 Hz.
Dies wurde farblich gekennzeichnet: z. B. Brüche 64 / 81 und 81 / 64
Der Ton F#/Gb lässt sich mit den Frequenzverhältnissen 729 / 1024 und 729 / 512 zum C mit 256 Hz nicht exakt spiegeln:
729 / 1024 * 512 Hz = 364,5 Hz <---> 1024 / 729 * 256 Hz = 359,593964335... Hz
729 / 512 * 256 Hz = 364,5 Hz <---> 512 / 729 * 512 Hz = 359,593964335... Hz
Mit ganzzahligen Brüchen ist dies auch nicht möglich, da hier eine irrationale Zahl benötigt wird.
In der Herleitung der Tonleiter über die Quinten und Quarten erscheint der Ton F#/Gb in der einen Richtung mit 364,5 Hz
Der geometrische Mittelwert zwischen diesen beiden Frequenzen ergibt:
Wurzel(364,5 Hz * 359,5939643347... Hz) = 362,038671968... Hz
Der Ton F#/Gb sollte exakt in der geometrischen Mitte zwischen den Tönen C einer Oktave liegen:
Wurzel(256 Hz * 512 Hz) = 362,038671968... Hz
Die Frequenz für den Ton F#/Gb kann auch mit der irrationalen Zahl Wurzel(2) = 1,41421356237... berechnet werden:
256 Hz * Wurzel (2) = 362,038671968... Hz
512 Hz * 1/Wurzel (2) = 362,038671968... Hz
Der so angepasste Ton F#/Gb hat keine gemeinsamen Obertöne mit den Tönen C darunter und darüber.
Dadurch ergibt sich eine starke Dissonanz - die Töne sind nicht in Einklang - sie klingen für das Ohr unharmonisch.
Im Quintenzirkel oder in der Quintenspirale liegen die Töne C und F#/Gb einander gegenüber.
Damit ist eine Anpassung über den Ton F#/Gb sehr gut für eine Korrektur der Tonleiter geeignet.
| Ton | Verhältnis | Frequenz | 2x | 3x | 4x | 5x | 6x | 7x | 8x | 9x | 10x | 11x | 12x |
| C |
1 | 256 | 512 | 768 | 1024 | 1280 | 1536 | 1792 | 2048 | 2304 | 2560 | 2816 | 3072 |
| F# / Gb |
Wurzel(1*2) | 362,04 | 724,08 | 1086,12 | 1448,15 | 1810,19 | 2172,23 | 2534,27 | 2896,31 | 3258,35 | 3620,39 | 3982,43 | 4344,46 |
| C' |
2 |
512 | 1024 | 1536 | 2048 | 2560 | 3072 | 3584 | 4096 | 4608 | 5120 | 5632 | 6144 |
Da der Ton F#/Gb in der originalen Pythagoräischen Scale nach dieser Überlegung nicht genau passt, habe ich dies in folgender Tabelle korrigiert.
Die Frequenzverhältnisse spiegeln sich dann auch exakt bei allen Tönen.
Harmonische Stimmung – Pythagoräische Scale – nur Halbton F#/Gb in der geometrischen Mitte zwischen den C's der Oktaven berechnet, exakte Spiegelung beim LOG2-Frequenzverhältnis (hier spielen)
| Ton | Frequenz | Primfaktoren | Frequenz- | Frequenz- | Frequenz- | Frequenz- | Quarten | Quinten |
| [Hz] | Verhältnis | Verhältnis | Verhältnis | Verhältnis | Rein = 4 / 3 | Rein = 3 / 2 | ||
| Ton (n+1)/n | zum C 256 | zum C 256 | zum C 256 | = 1,333... | = 1,500... | |||
| Dezimal | Bruch bzw. Wurzel | Dezimal | LOG2 | |||||
| C | 128,000000 | 3⁰ * 2⁷ | 1,053498 | 1 / 2 | 0,500000 | -1,000000 | 1,333333 | 1,500000 |
| C# / Db | 134,847737 | 2¹⁵ / 3⁵ | 1,053498 | 128 / 243 | 0,526749 | -0,924813 | 1,333333 | 1,489871 |
| D | 144,000000 | 3² * 2⁴ | 1,067871 | 9 / 16 | 0,562500 | -0,830075 | 1,333333 | 1,500000 |
| D# / Eb | 151,703704 | 2¹² / 3³ | 1,053498 | 16 / 27 | 0,592593 | -0,754888 | 1,333333 | 1,500000 |
| E | 162,000000 | 3⁴ * 2¹ | 1,067871 | 81 / 128 | 0,632813 | -0,660150 | 1,333333 | 1,500000 |
| F | 170,666667 | 2⁹ / 3¹ | 1,053498 | 2 / 3 | 0,666667 | -0,584963 | 1,333333 | 1,500000 |
| F# / Gb | 181,019336 | Wurzel(2⁷ * 2⁸) | 1,060660 | 1/Wurzel(2) * C | 0,707107 | -0,500000 | 1,342398 | 1,489871 |
| G | 192,000000 | 3¹ * 2⁶ | 1,060660 | 3 / 4 | 0,750000 | -0,415037 | 1,333333 | 1,500000 |
| G# / Ab | 202,271605 | 2¹⁴ / 3⁴ | 1,053498 | 64 / 81 | 0,790123 | -0,339850 | 1,333333 | 1,500000 |
| A | 216,000000 | 3³ * 2³ | 1,067871 | 27 / 32 | 0,843750 | -0,245112 | 1,333333 | 1,500000 |
| A# / Bb | 227,555556 | 2¹¹ / 3² | 1,053498 | 8 / 9 | 0,888889 | -0,169925 | 1,333333 | 1,500000 |
| B | 243,000000 | 3⁵ * 2⁰ | 1,067871 | 243 / 256 | 0,949219 | -0,075187 | 1,342398 | 1,500000 |
| C | 256,000000 | 3⁰ * 2⁸ | 1,053498 | 1 / 1 | 1,000000 | 0,000000 | 1,333333 | 1,500000 |
| C# / Db | 269,695473 | 2¹⁶ / 3⁵ | 1,053498 | 256 / 243 | 1,053498 | 0,075187 | 1,333333 | 1,489871 |
| D | 288,000000 | 3² * 2⁵ | 1,067871 | 9 / 8 | 1,125000 | 0,169925 | 1,333333 | 1,500000 |
| D# / Eb | 303,407407 | 2¹³ / 3³ | 1,053498 | 32 / 27 | 1,185185 | 0,245112 | 1,333333 | 1,500000 |
| E | 324,000000 | 3⁴ * 2² | 1,067871 | 81 / 64 | 1,265625 | 0,339850 | 1,333333 | 1,500000 |
| F | 341,333333 | 2¹⁰ / 3¹ | 1,053498 | 4 / 3 | 1,333333 | 0,415037 | 1,333333 | 1,500000 |
| F# / Gb | 362,038672 | Wurzel(2⁸ * 2⁹) | 1,060660 | Wurzel(2) * C | 1,414214 | 0,500000 | 1,342398 | 1,489871 |
| G | 384,000000 | 3¹ * 2⁷ | 1,060660 | 3 / 2 | 1,500000 | 0,584963 | 1,333333 | 1,500000 |
| G# / Ab | 404,543210 | 2¹⁵ / 3⁴ | 1,053498 | 128 / 81 | 1,580247 | 0,660150 | 1,333333 | 1,500000 |
| A | 432,000000 | 3³ * 2⁴ | 1,067871 | 27 / 16 | 1,687500 | 0,754888 | 1,333333 | 1,500000 |
| A# / Bb | 455,111111 | 2¹² / 3² | 1,053498 | 16 / 9 | 1,777778 | 0,830075 | 1,333333 | 1,500000 |
| B | 486,000000 | 3⁵ * 2¹ | 1,067871 | 243 / 128 | 1,898438 | 0,924813 | 1,342398 | 1,500000 |
| C | 512,000000 | 3⁰ * 2⁹ | 1,053498 | 2 / 1 | 2,000000 | 1,000000 | 1,333333 | 1,500000 |
Merkmale:
- A auf 432 Hz, wenn C auf 256 Hz, viele "heilige" Zahlen bei den Frequenzen der Töne
- Töne C, G, D, A, E, B sind aus dem Produkt der Primzahl-Potenzen von 2 (Oktaven-Sprung *2) und 3 (Quinten-Sprung *3/2) ableitbar 3^m*2^n
- Töne C#/Db, G#/Ab, D#/Eb, A#/Bb, F sind aus dem Quotient der Primzahlen-Potenzen von 2 (Oktaven-Sprung *2) und 3 (Quinten-Sprung *2/3) ableitbar 2^m/3^n
- exakte Spiegelung aller Töne beim LOG2-Frequenzverhältnis
- Ton F#/Gb liegt exakt in der geometrischen Mitte zwischen den Tönen C einer Oktave (Korrekturton)
- 11 von 13 reine Quarten in der Oktave, 2 Quarten mit kleinerer Abweichung (kaum wahrnehmbar)
- 11 von 13 reine Quinten in der Oktave, 2 Quinten mit kleinerer Abweichung (kaum wahrnehmbar)
- viele exakte Obertonüberlagerungen (Quarten und Quinten) und damit viel Harmonie
--> diese Instrumentenstimmung (von mir hergeleitet und angepasst) wäre sehr harmonisch für das Ohr und auch nach den Gesichtspunkten
der Heiligen Geometrie und den Zahlensystemen der Schöpfung (Primzahlen, heilige Zahlen und Zahlenverhältnissen)
sehr gut als Ersatz für die Musik der westlichen Welt geeignet.
In der Praxis müssten dafür aber die Instrumente und deren Tonstufen geringfügig angepasst werden.
Bei Instrumenten mit der Pythaoräischen Stimmung müsste nur der Ton F#/Gb minimal angepasst werden.
Grafik: Harmonische Stimmung – Pythagoräische Scale – nur Halbton F#/Gb in der geometrischen Mitte zwischen den C's der Oktaven berechnet
Die Geogebra-Grafik stellt die Töne und deren Frequenzen auf einer Logarithmischen Spirale (2er Logarithmus) dar:
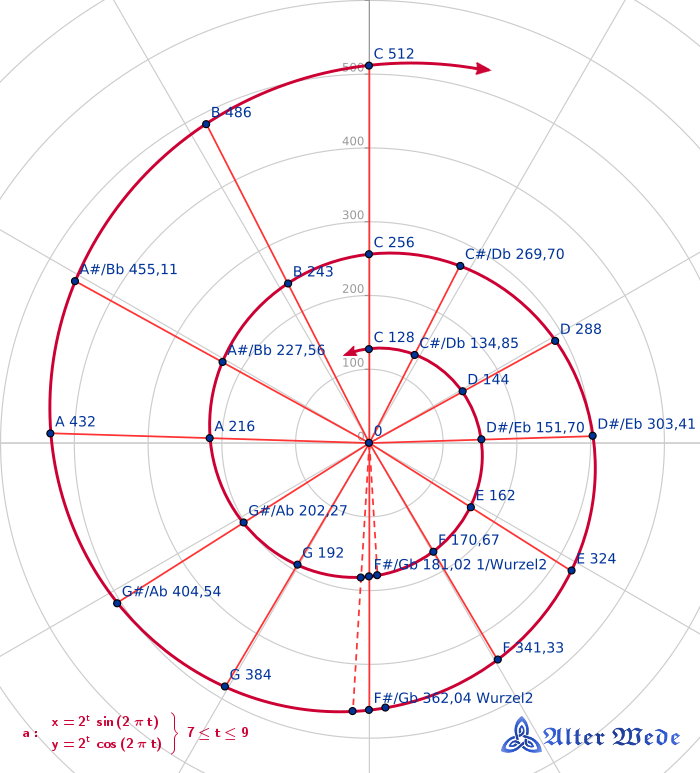
Diese Spirale kann auch als Oktav-Spirale bezeichnet werden - für jeden Punkt oder Ton auf dieser Spirale
ergibt sich nach einer Spiral-Umdrehung (360°) nach außen die doppelte oder nach innen die halbe Tonhöhe / Frequenz.
Die Spirale kann beliebig nach außen und nach innen erweitert werden. Die Töne liegen jeweils auf den Schnittpunkten der "logarithmischen
Spirale" mit den "orangefarbenen Linien aus dem Zentrum". Der Ton F#/Gb liegt in dieser harmonischen Stimmung exakt gegenüber vom Ton C.
Die gestrichelten Linien beim Ton F#/Gb zeigen den Ton mit reinen Quinten bzw. Quarten (z. B. 364,5 Hz oder 359,5939643347... Hz), wie er in
der ursprünglichen Pythagoräischen Scale verwendet wurde. In einer Richtung ergeben sich hierbei reine Quinten bzw. Quarten für den Ton F#/Gb,
in der anderen Richtung jedoch eine starke Abweichung von den reinen Quinten bzw. Quarten (große Dishamonie). Damit die harmonischen Zahlen und
Zahlenverhältnisse der Töne erhalten bleiben und dennoch eine oktavierbare harmonische Tonleiter-Spirale entsteht, wurde der Ton F#/Gb
auf den geometrischen Mittelwert zwischen den beiden Frequenzen (gestrichelte Linien) gelegt (geringe Disharmonie):
Wurzel(364,5 Hz * 359,5939643347... Hz) = 362,038671968... Hz
Dies ist mein Ansatz für eine harmonische Instrumentenstimmung als Ersatz für die Musik in der westlichen Welt:
Harmonische Instrumentenstimmung: C 256Hz und A 432Hz Stimmung, Ton-Frequenzen entstehen aus Potenzen der Primzahlen 2 und 3,
mit 11 von 13 reinen Quinten bzw. Quarten, Ton F#/Gb liegt exakt in der geometrischen Mitte zwischen den Tönen C
einer Oktave, exakte Spiegelung aller Töne beim LOG2-Frequenzverhältnis - Urheber: Alter Wede
Es sei noch erwähnt, dass es in anderen Kulturen ganz andere Tonsysteme gibt, die für den westlichen Menschen oft schräg klingen.
Diese haben jedoch einen ähnlichen systematischen und auch harmonischen Aufbau, doch sind wir weniger an diese Harmonien gewöhnt.
Ein Beispiel für ein sehr gut entwickeltes System ist die indische Scale mit 22 Tönen (hier spielen). Die Tonleiter beginnt bei dem Ton "Sa".
Die 7 Haupttöne (Sarvas) in einer Oktave sind Sa Ri Ga Ma Pa Dha Ni (Sa), alle anderen sind Mikrotöne (Shrutis).

Auf der Webseite whatmusicreallyis.com hat Bo Constantinsen sehr viel Grundlagenwissen über die Harmonie von Tönen veröffentlicht.
Dort wird in Form von vielen Grafiken der Aufbau von Tönen und Harmonie begreiflich gemacht.
Die Heilige Ton-Scale - Harmonisierung von 432 Hz, 528 Hz, 424 Hz und 440 Hz in einer einzigen Stimmung.
Natürlich Aufsteigende Reihe der Harmonischen 32 bis 64 (hier spielen).
weiterführende Quellen:
Ein Instrumenten-Entwurf für Experimente mit einer Vielzahl von Tonsystemen:
terpstrakeyboard.com
Mit diesem Online-Keyboard nach dem Vorbild des Terpstra-Keyboard können diverse Tonsysteme ausprobiert und auch selbst programmiert werden.
Oben wurden die verschiedenen Stimmungen auf das Online-Keyboard übertragen und können jeweils über den Link (hier spielen) getestet werden.
Das Online-Keyboard kann über die Tasten der Tastatur, mit der Maus oder ideal mit einem Touchpad gespielt werden:
terpstrakeyboard.com/web-app/keys.htm
Seite vom Erfinder des Terpstra-Keyboard mit Artikeln über diverse Tonsysteme:
siementerpstra.com/articles/
Englische Seite über das Thema "Was Musik wirklich ist":
whatmusicreallyis.com
Vortrag von Johann Oldenkamp über Wholly Science:
youtu.be/5f78IRk1xNQ?t=34m00s
Software Scala
huygens-fokker.org/scala/downloads.html
Software Baudline für Echtzeit Audio Spektrogramme (Linux, Mac OS)
baudline.com/download.html
Sonic Visualizer - Audio Spektrogramme
sonicvisualiser.org/screenshots.html
432 Hz Musik von Ananda Bosman
432hertz.com/Universal_Dances.html
Die Chakraphon-Musikinstrumente von Joga Dass basieren auf dem natürlichen Kammerton C1 mit 256 Hz:
www.intunemusic.de
Peter Graus hat eine interessante Methode entwickelt, wie der eigene Herzschlag in Echtzeit
in Musik und Licht gewandelt wird. Damit können wir erfahren, was unser Herz uns sagt.
Peter Graus - Der Klang der Herzen (Vortrag)
| <<< StartSeite <<< | Impressum |
erstellt am: 22.09.2014
|